T1

100%

用循环语句完成 $A_i$ 的输入，在输入的同时用 $\%2$ 操作判断是否是奇数，如果是奇数就更新答案。

注意判断 $A_i$ 中未出现奇数的情况。

T2

100%

首先当 $n\times m$ 是奇数时，无法恰好覆盖，证明如下：

$1\times 2$ 的砖块面积为 $2$，所以覆盖的总面积也一定是 $2$ 的整数倍，也就是说覆盖的面积只能是偶数不能是奇数。

而 $n\times m$ 是偶数时，存在恰好覆盖的方案，以下是其中一种方案：

因为 $n\times m$ 是偶数，所以 $n$ 和 $m$ 中至少有一个是偶数。

若 $n$ 是偶数，我们把砖块竖着放置，每行 $m$ 块，放 $\frac{n}{2}$ 行，如下方左图。

若 $m$ 是偶数，我们把砖块横着放置，每行 $\frac{m}{2}$ 块，放 $n$ 行，如下方右图。

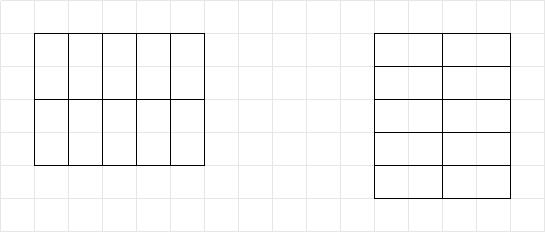
所以直接判断 $n\times m$ 的奇偶性即可。

T3

30%

先用两重循环枚举区间的左端点 $l$ 和右端点 $r$，再用一重循环进行区间内 $A_i$ 的求和。

时间复杂度 $O(n^3)$。

60%

预处理 $A_i$ 的前缀和 $sum[i] = \sum_{j=1}^i A_j = A_1 + A_2+……+A_i$。

用两重循环枚举区间的左端点 $l$ 和右端点 $r$，用 $sum[r]-sum[l-1]$ 来 $O(1)$ 求出区间和。

注意最终答案可能会爆 $\text{int}$。

时间复杂度 $O(n^2)$。

100%

从贡献的角度：考虑 $A_i$ 在哪些区间里会对答案分别产生什么样的影响。

如果区间包含 $i$，那么会让答案增加 $A_i$。即贡献为 $l\leq i \leq r$ 的区间的数量，乘上 $A_i$。

此时 $l$ 和 $r$ 的取值范围是独立的， $l$ 的取值范围为 $1\sim i$， $r$ 的取值范围为 $i\sim n$，所以这样的区间共有 $i\times (n-i+1)$ 个。

所以最终答案为 $\sum_{i=1}^n A_i\times i\times (n-i+1)$。注意不仅最终答案会爆 $\text{int}$，过程中也可能爆 $\text{int}$。

时间复杂度 $O(n)$。

T4

30%

对于测试点#3~5，按照题目所说，对每个询问，模拟过程中的位置变化即可。

记 $c_i$ 最大值为 $C=\max\{c_i\}$。

时间复杂度 $O(qC)$。

50%

对于测试点#1~2，可以用 $f[i][j]$ 维护从 $i$ 出发， $j$ 秒之后所在的位置。转移式为 $f[i][j]=f[f[i][j-1]][1]$。

时间复杂度 $O(nC)$。

结合第一部分可以拿到 $50\%$ 的分数。

时间复杂度 $O(\min(qC, nC))$。

100%

按照倍增的思路，用 $f[i][j]$ 维护从 $i$ 出发， $2^j$ 秒之后所在的位置。转移式为 $f[i][j]=f[f[i][j-1]][j-1]$。

用倍增的思路，将每个询问分解为若干个时间长度为 $2$ 的幂的步骤（比如 $21=2^0+2^2+2^4$），通过之前维护的 $f$ 数组模拟每个步骤的位置变化。

时间复杂度 $O(n\log (C)+q\log(C))$。

T5

20%

用两重循环枚举区间的左端点 $l$ 和右端点 $r$，对区间内的元素进行排序，如果第 $k$ 小的元素大于等于 $x$ 那么最终答案增加 $1$。

时间复杂度 $O(n^3\log(n))$。

50%

“区间内第 $k$ 小的元素大于等于 $x$ ”可以转化为“区间内小于 $x$ 的元素少于 $k$ 个”。

用 $sum[i]$ 维护前缀 $[1,i]$ 中小于 $x$ 的元素的个数。

用两重循环枚举区间的左端点 $l$ 和右端点 $r$，用 $sum[r]-sum[l-1]$ 求出区间内小于 $x$ 的元素的个数，如果少于 $k$ 个那么最终答案增加 $1$。

时间复杂度 $O(n^2)$。

100%

• 方法1：

对于同一个左端点 $l$，区间内小于 $x$ 的元素的个数是随着右端点 $r$ 的增大而递增的。

因此对于每个 $l$，我们可以用二分右端点 $r$，用上述方法进行check，找出最大的 $r$ 满足 $[l,r]$ 是过分子的区间，即对于左端点 $l$，右端点取 $[l,r]$ 时都是过分的子区间，答案增加 $r-l+1$。

时间复杂度 $O(n\log(n))$。

• 方法2：

不难发现这个满足条件的最大的右端点 $r$，也是随着左端点 $l$ 的增大而递增的，因此我们可以用双指针的思路来求出每个 $l$ 对应的最大的 $r$。

时间复杂度 $O(n)$。

• 方法3：

预处理第 $i$ 个满足 $A[j]<x$ 的位置 $pos[i]$，枚举 $pos[i]$ 作为区间内第一个小于 $x$ 的元素所在位置，那么对应的过分子区间的左端点取值范围为 $[pos[i-1]+1,pos[i]]$，右端点的取值范围为 $[pos[i],pos[i+k]-1]$。

另外还有一类过分的子区间是不包含小于 $x$ 的元素的，枚举左端点 $l$，设 $l$ 右侧最近的小于 $x$ 的元素位置为 $g$，那么右端点的取值范围为 $[l,g-1]$。

时间复杂度 $O(n)$。

T6

20%

对于测试点#1~2，因为 $m=10$ 所以可以直接从 $n$ 个 $0$ 到 $n$ 个 $9$ 枚举答案，枚举后再统计每一种数字的出现次数，判断是否满足出现次数都不超过 $k$ 的限制。

时间复杂度 $O(m^nn)$。

30%

对于测试点#1~3，可以用 $\text{DFS}$ 或其他方法，从 $n$ 个 $0$ 到 $n$ 个 $m-1$ 枚举答案，枚举的同时统计每种数字的出现次数。如果用 $\text{DFS}$ 来实现，前缀不满足条件时还可以直接剪枝。

时间复杂度 $O(m^n)$。

40%

对于测试点#1和测试点#4，因为 $k=n$ 所以答案就是 $m^n$。注意最终答案可能会爆 $\text{int}$，要取模。

时间复杂度 $O(n)$。

结合第二部分可以拿到 $40\%$ 的分数。

100%

将问题转化为在 $n$ 个空位分别填入 $0\sim m-1$ 这 $m$ 种数字。用 $dp[i][j]$ 表示用前 $i$ 种数字（即 $0\sim i-1$ ）填了 $j$ 个位置的方案。

考虑前 $i-1$ 种数字已经填了 $j$ 个位置，在剩下的 $n-j$ 个位置中再选 $p$ 个位置填第 $i$ 种数字，那么转移方程为 $dp[i][j+p]+=dp[i-1][j]\times \binom {n-j} {p}$。

另一种思路是考虑前 $i$ 种数字填 $j$ 个位置，其中第 $i$ 种数字占 $p$ 个位置，那么转移方程为 $dp[i][j]=\sum_{p=0}^{k} dp[i-1][j-p]\times \binom {n-(j-p)} {p}$。

组合数可以用杨辉三角法预处理。注意过程中的取模和爆 $\text{int}$ 问题。

时间复杂度 $O(mnk)$。