T1

100%

用循环语句输入 $A_i$ 的时候判断一下是否等于 $x$，如果 $A_i=x$ 答案就增加 $1$。

注意数据范围，$x$ 和 $A_i$ 应使用 $\text{long long}$ 类型的变量来读入和处理。

时间复杂度 $O(n)$。

T2

100%

两重循环，外层循环枚举数组第 $i$ 项，内层循环计算 $A_i$ 的 $k$ 次幂。

注意取模，计算其中一项 $k$ 次幂的过程中也可能爆 $\text{int}$。

时间复杂度 $O(nk)$。

T3

50%

记 $V=\min(a,b)$。

直接从 $1$ 到 $V$ 枚举 $x$，如果 $x$ 是 $a$ 和 $b$ 的公因数，答案就增加 $x$。

时间复杂度 $O(V)$。

60%

对于测试点#6，因为 $a=b$，所以 $a$ 和 $b$ 的公因数等价于 $a$ 的因数，找出 $a$ 的所有因数再加起来就是答案了。

找 $a$ 的因数时， $x$ 只需要枚举到 $\sqrt{a}$，如果 $x$ 是 $a$ 的因数那么 $\frac{a}{x}$ 也是 $a$ 的因数。注意判断 $x=\frac{a}{x}$ 的情况，不要加重复了。

时间复杂度 $O(\sqrt {a})$。

结合第一部分可以拿到 $60\%$ 的分数。

100%

先求出 $a$ 和 $b$ 的公因数 $c=\gcd(a,b)$， $a$ 和 $b$ 的公因数等价于 $c$ 的因数。显然 $c\leq V$。

找 $c$ 的因数时，同样只需要枚举到 $\sqrt{c}$。

时间复杂度 $O(\sqrt {V})$。

T4

30%

假设 $a,b,c$ 三根木棍的长度满足 $len_a\leq len_b\leq len_c$，那么当且仅当 $len_a+len_b>len_c$ 时这三根木棍可以搭成面积大于 $0$ 的三角形。

直接三重循环枚举三根木棍，用上述规则进行判断，符合则答案增加 $1$。

注意三根木棍编号不能相同，还要避免重复枚举同一个方案。

时间复杂度 $O(n^3)$。

50%

将木棍按照长度从短到长排序。

先用两重循环枚举更短的两根木棍 $a$ 和 $b$ ($a<b$)，那么只要 $len_c<len_a+len_b$ 就可以了，用二分法求出共有多少根木棍可以和 $a,b$ 一起搭成面积大于 $0$ 的三角形。

要避免重复枚举同一方案，所以只有满足 $c>b$ 才是可选的 $c$。

时间复杂度 $O(n^2\log(n))$。

70%

对于测试点#6~7，预处理长度不超过 $x$ 的木棍数量为 $sum[x]$。

用两重循环枚举 $a$ 和 $b$ 之后，可选的 $c$ 的数量就等于$sum[len_a+len_b-1]-b$。

注意虽然 $len$ 的范围是 $10^6$，但是 $len_a+len_b$ 有可能达到 $2\times 10^6$，所以预处理 $sum$ 数组时要预处理到 $2\times 10^6$，或者特判 $len_a+len_b>10^6$ 的情况。

记 $len_i$ 的最大值为 $L=\max\{len_i\}$。

时间复杂度 $O(L+n^2)$。

结合第二部分可以拿到 $70\%$ 的分数。

100%

当 $a$ 不变时，随着 $b$ 的增大， $len_a+len_b$ 也是增大的。

所以在木棍按长度排序之后，我们可以把 $b$ 和 $c$ 看成双指针，当 $b$ 右移时，尽量右移 $c$ 直到 $c=n$ 或者 $len_a+len_b\leq len_{c+1}$ 时停下。

相当于在第二部分的基础上，用双指针代替二分法，来求出有多少根木棍可以作为 $c$。

时间复杂度 $O(n^2)$。

T5

20%

枚举每个知识点学与不学，那么共有 $2^n$ 个不同的方案，然后 $O(n)$ 判断方案中每个选择学的知识点是否满足前置知识点都学习了，用合法方案的价值和更新答案。

时间复杂度 $O(2^nn)$。

60%

因为每个知识点最多只会有一个前置知识点，可以把这类前置关系看成树的结构，$p_i$ 是 $i$ 的父节点。

用 $dp[i][j]$ 表示以 $i$ 为根的子树中，学 $j$ 个知识点的最大价值。我们枚举节点 $x$ 的子节点 $y$，用 $tmp[x][i]$ 表示以 $x$ 为根的子树已经处理过的部分（即不包括 $y$ 等未处理的子节点和以它们为根的子树）中，学 $i$ 个知识点的最大价值。那么 $tmp[x][a+b]=\max\{tmp[x][a]+dp[y][b]\}$，这里 $a$ 至少是 $1$，因为不学知识点 $x$ 就无法学习子树内其他知识点。

由于可能存在多个 $p_i=0$ 的知识点，可以把 $0$ 看成树的根，那么答案就是 $dp[0][m+1]$。

实际实现中，$tmp$ 和 $dp$ 可以是同一个数组，原理同01背包的一维写法，此时需要按 $a+b$ 从大到小的顺序更新，记 $s=a+b$，参考代码如下：

for (int s = m + 1; s >= 1; s--)
	for (int b = 1; b < s; b++) {
		int a = s - b;
		dp[x][s] = max(dp[x][s], dp[x][a] + dp[y][b]);
	}

时间复杂度 $O(n^3)$。

100%

用 $siz[i]$ 表示以 $i$ 为根的子树中知识点数量， $tmpsiz[i]$ 表示以 $i$ 为根的子树已经处理过的部分中知识点的数量。

如果限制 $a\leq tmpsiz[x]$ 且 $b\leq siz[y]$，可以证明总复杂度会降低到 $O(n^2)$：

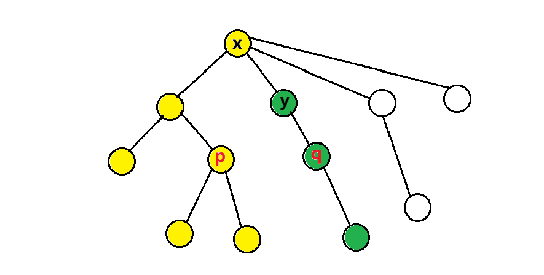
这一过程的复杂度等价于在两个部分各选一个点的方案数，不难发现任意一对点在这个过程中只会在LCA(最近公共祖先)处被考虑一次，所以总复杂度是 $O(n^2)$。

如下图，点对 $(p,q)$ 仅在 $LCA(p,q)=x$ 时被考虑，其中黄色点是以 $x$ 为根的子树已经处理过的部分，绿色点是以 $y$ 为根的子树。

参考代码如下：

for (int s = siz[x] + siz[y]; s >= 1; s--) {
	for (int b = max(s - siz[x], 0); b <= siz[y] && b < s; b++) {
        int a = s - b;
		dp[x][s] = max(dp[x][s], dp[x][a] + dp[y][b]);
	}

时间复杂度 $O(n^2)$。

T6

10%

三重循环，外层两重循环枚举子区间 $[l,r]$，内层再用一重循环求出区间和 $sumA(l,r)=\sum_{i=l}^{r} A_i$，如果满足 $avg(l,r)\geq x$ 的条件就把区间和加到答案上。

注意取模。

可以不计算平均值，用区间和直接与 $x\times (r-l+1)$ 进行比较。

时间复杂度 $O(n^3)$。

30%

预处理前缀和，就可以 $O(1)$ 计算区间和。这样只需要两重循环枚举子区间。

时间复杂度 $O(n^2)$。

50%

处理出数组 $B_i=A_i-x$，记 $B_i$ 的区间和为 $sumB(l,r)=\sum_{i=l}^{r} B_i$，那么子区间 $[l,r]$ 满足条件等价于 $sumB(l,r)\geq 0$。

枚举子区间右端点 $r$，对于满足 $sumB(l,r)\geq 0$ 的每一个左端点 $l$，答案增加 $sumA(l,r)$，这个做法和第二部分类似。

在这个基础上，把 $sumA(l,r)$ 分解为 $sumA(1,r)$ 和 $-sumA(1,l-1)$ 两部分。

$sumB(l,r)\geq 0$ 也可以转化为 $sumB(1,r)\geq sumB(1,l-1)$，称为对于 $r$ 合法的 $l$。

那么第一部分对答案贡献的次数为对于 $r$ 合法的 $l$ 的数量。

第二部分对答案的总贡献为每个对于 $r$ 合法的 $l$ 都让答案增加 $-sumA(1,l-1)$。

将 $B_i$ 的前缀和的值作为下标，用权值线段树分别维护 $sumB(1,i)=j$ 对应的 $i$ 的数量以及对应的 $\sum sumA(1,i-1)$，就可以枚举 $r$，分别计算以上两部分了。

记 $B_i$ 的前缀和的跨度为 $V=\max\{sumB(1,i)\}-\min\{sumB(1,i)\}$。

时间复杂度 $O(n\log(V))$。

结合第二部分可以拿到 $50\%$ 的分数。

60%

对于测试点#6，因为 $x\leq \min\{A_i\}$，所以每个区间都满足条件。

答案就等于所有子区间的区间和之和。

时间复杂度 $O(n)$。

结合第二、第三部分可以拿到 $60\%$ 的分数。

100%

在第三部分的基础上，将下标域扩展到 $[-10^{12},10^{12}]$。

• 方法1：

使用动态开点的权值线段树。

时间复杂度 $O(n\log(V))$。

• 方法2：

计算出 $B_i$ 的所有前缀和之后，进行离散化，然后以离散化后的权值为下标建线段树。

时间复杂度 $O(n\log(n))$。