T1

100%

读入字符串 $S$，用循环语句枚举字符串 $S$ 的第 $i$ 位，如果 $S$ 的 $i,i+1,i+2$ 这三位恰好是 wow，那么答案加一。

注意 $i$ 的循环范围，要避免 $i+2$ 越界，同时注意字符串的下标是从 $0$ 还是从 $1$ 开始。

时间复杂度 $O(n)$。

T2

100%

$0\sim n$ 共有 $n+1$ 个数字，其中至少有一个数字没在 $A$ 中出现。所以 $A$ 的 $\text{MEX}$ 不超过 $n$。

这意味着我们只需要考虑 $A_i\leq n$ 的情况。

先循环第一次遍历 $A$，对于所有满足 $A_i\leq n$ 的元素，用数组 $B$ 标记它在 $A$ 中是否出现过。$B[x]=1$ 表示 $x$ 在 $A$ 中出现过，$B[x]=0$ 表示 $x$ 在 $A$ 中没有出现过。

再循环第二次遍历 $B$，答案即为最小的满足 $B[x]=0$ 的 $x$。

时间复杂度 $O(n)$。

T3

50%

用一个二维数组 $f[i][j]$ 记录 $i$ 和 $j$ 是否有矛盾。

两重循环模拟分班过程：外层循环按从 $1$ 到 $n$ 的顺序枚举第 $x$ 个人，内层循环枚举在 $x$ 之前已经完成分班的 $y$，如果 $x$ 和 $y$ 有矛盾，那么 $x$ 不能分到 $y$ 所在的班。可以用 $2$ 个变量分别表示 $x$ 能否分到1班和2班，按题目所说的规则决定 $x$ 去哪个班并记录下来用于后续判断，同时维护两个班的总团结度变化。

时间复杂度 $O(n^2)$。

100%

在第一部分的基础上，用邻接表代替二维数组：$vec[i]$ 中记录和 $i$ 有矛盾且在 $i$ 之前完成分班的人。

在模拟分班的过程中，当外层循环枚举到第 $x$ 个人分班时，内层循环改为枚举 $vec[x]$ 中的元素。

由于每条矛盾关系只会让 $vec[\max(u_i,v_i)]$ 增加一个元素，所以 $n$ 个 $\text{vector}$ 内一共有 $m$ 个元素，空间复杂度 $O(n+m)$。

时间复杂度 $O(n+m)$。

T4

20%

暴力计算出矩阵 $C$ 中每个数字，对其排序后求出区间和。

时间复杂度 $O(nm\log(nm))$。

40%

对于测试点#3~4，因为 $A_i,B_i\leq 2000$，所以 $C(i,j)\leq 4\times 10^6$。

用数组 $cntA[x]$ 记录数字 $x$ 在 $A$ 中出现了多少次，数组 $cntB[x]$ 记录数字 $x$ 在 $B$ 中出现了多少次。

可以维护出表示数字 $x$ 在 $C$ 中出现了多少次的数组 $cntC[x]$：枚举 $i$ 和 $j$，$cntC[i\times j]$ 增加 $cntA[i]\times cntB[j]$。

定义 $ask(k)$ 表示前 $k$ 小的数字的和，将区间和转化为两个前缀和的差分，答案即为 $ask(R)-ask(L-1)$。

$ask(k)$ 可以通过循环遍历 $cntC$ 来计算。

记 $A_i$ 的最大值为 $V_A=\max\{A_i\}$，$B_i$ 的最大值为 $V_B=\max\{B_i\}$。

时间复杂度 $O(V_AV_B)$。

结合第一部分可以拿到 $40\%$ 的分数。

60%

对于测试点#5~6，因为 $L=1$，所以答案就是 $ask(R)$。我们只需要考虑如何计算 $ask(R)$。

记矩阵 $C$ 中，满足 $C(i,j)\leq x$ 的元素数量为 $num(x)$，满足 $C(i,j)\leq x$ 的元素之和为 $sum(x)$。

$num(x)$ 可以用二分来计算：

• 先将 $B$ 按从小到大的顺序排序；
• 枚举 $A$ 的下标 $i$，二分求出满足 $A_i\times B_j \leq x$ 的最大的 $j$，将 $j$ 加到返回值中。

用上述方法求一次 $num(x)$ 的时间复杂度为 $O(n\log(m))$。

求 $sum(x)$ 的方法类似求 $num(x)$ 的方法：

• 先将 $B$ 都按从小到大的顺序排序，处理出排序后 $B$ 的前缀和 $Bsum[i]$；
• 枚举 $A$ 的下标 $i$，二分求出满足 $A_i\times B_j \leq x$ 的最大的 $j$，将 $A[i]\times B[1]+A[i]\times B[2]+\dots+A[i]\times B[j]=A[i]\times(B[1]+B[2]+\dots+B[j])=A[i]\times Bsum[j]$ 加到返回值中。

这样就可以二分求满足 $num(val)\geq R$ 的最小的 $val$，这个 $val$ 也就是第 $R$ 小的那一项的值。

求出 $val$ 之后，$sum(val)$ 即为前 $num(val)$ 小的数字的和。对于 $num(val)>R$ 的情况，因为第 $R$ 小和第 $num(val)$ 小的数字都等于 $val$，所以第 $R+1$ 小到 $num(val)$ 小的数字都等于 $val$，减去这部分即可。

答案 $ask(R)=sum(val)-val\times (num(val)-R)$。

时间复杂度 $O(n\log(V_AV_B)\log(m))$。

结合第一、第二部分可以拿到 $60\%$ 的分数。

100%

在第三部分的基础上，将区间和转化为两个前缀和的差分，答案即为 $ask(R)-ask(L-1)$。

时间复杂度 $O(n\log(V_AV_B)\log(m))$。

T5

40%

枚举 $p$，以 $p$ 为起点 $\text{DFS}$ 整棵树，过程中维护到每个节点的距离，计算答案。

时间复杂度 $O(n^2)$。

60%

设 $p=i$ 时的答案为 $ans_p=\sum_{i=1}^na_i\times \text{dis}(p,i)$。

对于测试点#5~6，因为 $a_i=1$ 且 $l_i=1$，所以答案就是每个节点到 $p$ 的距离之和。

将树看成以 $1$ 为根的有根树，用 $siz[i]$ 表示以 $i$ 为根的子树内的节点数量。考虑 $ans_y$ 和 $ans_x$ 的关系，这里节点 $x$ 是节点 $y$ 的父节点，如下图所示：

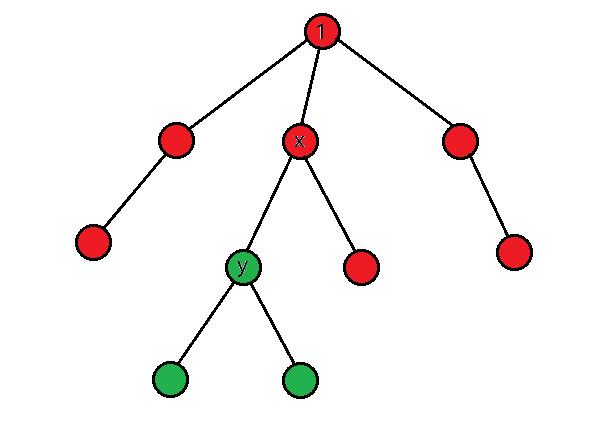
考虑 $p$ 从 $x$ 变成 $y$，那么图中红色的节点到 $p$ 的距离增加 $1$，绿色的节点到 $p$ 的距离减少 $1$。绿色的节点即是以节点 $y$ 为根的子树内的节点，数量为 $siz[y]$；红色的节点数量为 $n-siz[y]$。因此 $ans_y=ans_x+(n-siz[y])-siz[y]$。

因此只需要先从节点 $1$ 出发用 $\text{DFS}$ 计算出 $ans_1$ 以及 $siz[i]$ 数组，然后再进行第二次 $\text{DFS}$，计算出其他节点的答案。

时间复杂度 $O(n)$。

结合第一部分可以拿到 $60\%$ 的分数。

100%

考虑 $p$ 从 $x$ 变成 $y$，红色节点到 $p$ 的距离增加 $dis(x,y)$，绿色的节点到 $p$ 的距离减少 $dis(x,y)$。

用 $sum[i]$ 表示以 $i$ 为根的子树内的节点的权值之和，绿色节点总权值为 $sum[y]$，红色节点总权值为 $sum[1]-sum[y]$。

因此在第二次 $\text{DFS}$ 时，用 $ans_y=ans_x+dis(x,y)\times (sum[1]-sum[y])-dis(x,y)\times sum[y]$ 计算其他节点的答案即可。

时间复杂度 $O(n)$。

T6

20%

用 $ans[i]$ 表示 $i$ 对应的答案。

预先处理出数组 $pcnt[i]=\text{popcount}(A_i)$。

两重循环枚举 $i$ 和 $j$，枚举时注意 $i\leq j$，判断是否满足 $A_i\oplus A_j>X$ 和 $pcnt[i]\leq pcnt[j]$，如果都满足则 $ans[i]$ 增加 $1$。

记 $A_i$ 的最大值为 $V=\max\{A_i\}$。

时间复杂度 $O(n\log(V)+n^2)$。

50%

对于测试点#3~5，因为 $X,A_i\leq 1000$，可以直接预处理 $\text{bool}$ 数组 $f[Y][Z]$，其中 $f[Y][Z]=1$ 表示 $Y$ 和 $Z$ 满足 $Y\oplus Z>X$ 且 $\text{popcount}(Y)\leq \text{popcount}(Z)$，题目的三个条件就转化为 $j\geq i$ 且 $f[A_i][A_j]=1$。

从大到小枚举 $i$，同时维护 $cnt[x]$ 表示 $x$ 已经出现了多少次，对于每一个满足 $f[A_i][x]=1$ 的 $x$，$ans[i]$ 增加 $cnt[x]$。

时间复杂度 $O(nV)$。

结合第一部分可以拿到 $50\%$ 的分数。

100%

先不考虑 $pcnt[i]\leq pcnt[j]$ 这一条件，仅考虑余下两个条件，可以用 $\text{01trie}$ 来解决，将满足 $i\leq j\leq n$ 的每个 $A_j$ 都添加到字典树上后，$ans[i]$ 可以在字典树上查询。

在此基础上考虑 $pcnt[i]\leq pcnt[j]$ 这一条件，有以下两个方法：

• 方法1

开一个二维数组 $siz[j][k]$，记录字典树上节点 $j$ 对应的子树内，满足 $pcnt[i]=k$ 的 $i$ 的数量。

查询 $ans[i]$ 时，每当在字典树上走到节点 $j$，枚举 $k$ 满足 $k\geq pcnt[i]$，将 $siz[j][k]$ 加到答案中。

二维数组 $siz$ 的第一维如果开到 $n\times \log(V)$ 有可能会空间超限，可以证明第一维只需开到 $n\times 15$ 以上就足够了：字典树上对应二进制最高 $16$ 位的节点不超过 $2^{16+1}\leq n$ 个点，剩余节点不超过 $n\times (\log(V)-16)$ 个，而 $\log(V)\leq 30$，所以最多不超过 $n\times 15$ 个点。

时间复杂度 $O(n\log^2(V))$。

• 方法2

分 $\log(V)$ 轮计算答案，第 $k$ 轮只对满足 $\text{popcount}(A_i)=k$ 的 $i$ 求答案，所以第 $k$ 轮只将同时满足 $\text{popcount}(A_j)\geq k$ 和 $j\geq i$ 的 $A_j$ 添加到字典树上。

时间复杂度 $O(n\log^2(V))$。