T1

100%

枚举 $L\sim R$ 的每个数，如果 $\%K$ 的余数为 $0$ 说明是 $K$ 的倍数，答案增加一。

时间复杂度 $O(R-L)$。

T2

100%

两重循环遍历矩阵的每个格子，如果 $(i,j)$ 有炸弹，那么用以下方式找到这个炸弹能炸到的每个格子 $(x,y)$：

• 两重循环枚举 $x$ 和 $y$，其中 $x$ 的循环范围为 $i-3\sim i+3$，$y$ 的循环范围为 $y-3\sim y+3$；
• 判断 $(x,y)$ 是否超出矩阵边界，即需要同时满足 $1\leq x\leq n$ 和 $1\leq y\leq m$；
• 判断 $(x,y)$ 是否在 $(i,j)$ 炸的范围内，即还需要满足 $|x-i|+|y-i|\leq 3$，这里 $|x|$ 表示求 $x$ 的绝对值。

对于通过以上方式找到的每个 $(x,y)$，将 $(x,y)$ 的答案增加一。

时间复杂度 $O(nm)$。

T3

50%

两重循环枚举 $i,j$，将 $\gcd(i,N)\times \gcd(j,M)$ 加到答案中。

注意答案可能会超出 $\text{int}$ 范围。

注意取模。

时间复杂度 $O(NM(\log(N)+\log(M)))$。

100%

将 $\gcd(i,N)$ 作为公因式提取可得：

$\gcd(i,N)\times \gcd(1,M)+\gcd(i,N)\times \gcd(2,M)+\dots+\gcd(i,N)\times \gcd(M,M)$

$=\gcd(i,N)\times (\gcd(1,M)+\gcd(2,M)+\dots+\gcd(M,M))$

$=\gcd(i,N)\times \sum_{j=1}^M\gcd(j,M)$

所以我们可以先计算出 $S=\sum_{j=1}^M\gcd(j,M)$，答案就可以这样计算：

$\sum_{i=1}^N\sum_{j=1}^M(\gcd(i,N)\times \gcd(j,M))$

$=\sum_{i=1}^N(\gcd(i,N)\times \gcd(1,M)+\gcd(i,N)\times \gcd(2,M)+\dots+\gcd(i,N)\times \gcd(M,M))$

$=\sum_{i=1}^N(\gcd(i,N)\times \sum_{j=1}^M\gcd(j,M))$

$=\sum_{i=1}^N(\gcd(i,N)\times S)$。

注意答案可能会超出 $\text{long long}$ 范围。

注意过程中取模。

时间复杂度 $O(N\log(N)+M\log(M))$。

这个式子还可以继续化简，鼓励有兴趣的同学们自己试一试。

T4

40%

如果规定 $C$ 的最小值为 $X$，那么为了让极差取最小值，要想办法让 $C_i$ 取到大于等于 $X$ 的最小值。

对于 $1\sim n$ 中的每个 $i$，定义 $f(i,X)$ 为满足 $A_i+B_j\geq X$ 的最小的 $A_i+B_j$。

如果 $X$ 太大，有可能出现对于某个 $i$，不存在任何 $j$ 能满足 $A_i+B_j\geq X$ 的情况。因此对于 $1\sim n$ 中的每个 $i$，定义 $MAXC(i)$ 为 $A_i+B_j$ 的最大值，预先计算 $Limit=\min\{MAXC(i)\}$。这样只需限制 $X\leq Limit$ 就能保证 $f(i,X)$ 是可以正常计算的。

规定 $C$ 的最小值为 $X$ 时，定义 $C$ 的极差为 $Range(X)=\max\{f(i,X)\}-X$。那么答案就是 $\min\{Range(X)\}$。

因为最小值一定等于某个 $A_i+B_j$，所以我们可以用四重循环来求答案：

• 前两重循环枚举 $1\leq x\leq n$ 和 $1\leq y\leq m$，如果 $A_x+B_y\leq Limit$，那么规定最小值为 $A_x+B_y$，接下来计算 $Range(A_x+B_y)$；
• 第三重循环枚举 $1\leq i\leq n$；
• 第四重循环枚举 $1\leq j\leq m$，计算出 $f(i,A_x+B_y)$ 用来更新 $Range(A_x+B_y)$；
• 用 $Range(A_x+B_y)$ 更新答案。

时间复杂度 $O(n^2m^2)$。

60%

记 $A_i+B_j$ 的最大值为 $V_C=\max\{A_i+B_j\}$。显然 $Limit\leq V_C$。

记 $A_i$ 的最大值为 $V_A=\max\{A_i\}$。

对于测试点#5~6，因为 $A_i,B_i\leq 1000$，所以 $Limit\leq 2000$。

同时对于 $1\sim n$ 中的两个不同下标 $i$ 和 $j$，如果 $A_i=A_j$ 那么 $f(i,X)=f(j,X)$。所以对于数组 $A$ 中的相同数字，每种只需要保留一个就可以了，这样去重过后的数组 $A$ 规模不超过 $1000$。

这样我们就可以用三重循环来求答案：

• 第一重循环枚举 $1\leq X\leq Limit$，表示规定最小值为 $X$，接下来计算 $Range(X)$；
• 第二重循环在去重后的数组 $A$ 中枚举下标 $i$；
• 第三重循环枚举 $1\leq j\leq m$，计算出 $f(i,X)$ 用来更新 $Range(X)$；
• 用 $Range(X)$ 更新答案。

时间复杂度 $O(mV_CV_A)$。

结合第一部分可以拿到 $60\%$ 的分数。

100%

两重循环枚举 $1\leq x\leq n$ 和 $1\leq y\leq m$，将 $A_x+B_y$ 和对应的 $x$ 一起保存到结构体数组 $D$ 中，具体来说 $D[i].C=A_x+B_y$，$D[i].X=x$。按 $D[i].C$ 从小到大的顺序对 $D$ 进行排序。

规定 $C$ 的最小值为 $D[L].C$，找出最小的 $R$ 满足 $\{D[L].x,D[L+1].x,\dots,D[R].x\}$ 中 $1\sim n$ 都出现过至少一次，那么 $Range(D[L].C)=D[R].C-D[L].C$。

维护 $cnt[x]$ 表示当前区间内有多少个 $i$ 满足 $D[i].X=x$。

区间的初始左端点 $L=1$，右端点 $R$ 为最小的 $R$ 满足 $\{D[1].x,D[2].x,\dots,D[R].x\}$ 中 $1\sim n$ 都出现过至少一次。

当左端点从 $L$ 变为 $L+1$ 时，$D[L].X$ 的出现次数减少一次，所以 $cnt[D[L].X]$ 减一。如果 $cnt[D[L].X]$ 因此变成 $0$，那么不断将右端点向右移动，直到 $cnt[D[L].X]>0$。其中当右端点从 $R$ 变为 $R+1$ 时，$D[R+1].X$ 的出现次数增加一次，所以 $cnt[D[R+1].X]$ 加一。

如果右端点移动后能满足 $cnt[D[L].X]>0$，那么用 $Range(D[L+1].C)=D[R'].C-D[L+1].C$ 更新答案，这里的 $R'$ 为此时的右端点。这个过程用到了双指针算法，这部分的总时间复杂度为 $O(nm)$。

整个算法的时间复杂度瓶颈在于对结构体数组 $D$ 的排序。

时间复杂度 $O(nm\log(nm))$。

T5

30%

小球在移动的全过程中，相对顺序是不发生变化的。可以把小球的碰撞，看成是两个小球重合时交换编号，移动的方向不变。这一点也可以通过观察样例解释发现。

这样我们只需要求出初始时每个编号对应的排名，对每个球单独计算出 $t$ 秒后的最终位置，将最终位置再排序一次，结合编号对应的排名就可以得到每个编号的小球的最终位置。

时间复杂度 $O(n\log(n))$。

50%

不论有多少墙，都不影响小球的相对顺序，所以还是对每个球单独计算最终位置再排序。

对于测试点#4~5，因为最多有一个墙，所以只有初始位于墙左边且移动方向向右和初始位于墙右边且移动方向向左的球可能撞到墙，且最多因为撞墙而改变方向一次。对于这种情况，先计算撞墙的时间，再计算剩余时间反方向移动的距离，就可以算出最终位置了。

时间复杂度 $O(n\log(n))$。

100%

对于一个小球，如果它的左右都有墙，那么它可能会发生很多次撞墙。

将 $A$ 和 $B$ 都按从小到大排序，就可以用双指针的方法找到每个小球两边距离最近的墙的位置。

假设小球左边最近的墙的位置为 $L$，右边最近的墙的位置为 $R$，那么可以把它的移动过程分为三个阶段：

• 开始移动到第一次撞墙为止；
• 从第一次撞墙开始，每经过 $2\times(R-L)$ 秒，小球就会撞到另一个墙并回到第一次撞墙的位置，所以每 $2\times(R-L)$ 秒一个周期；
• 最后可能还剩一个不完整的周期。

先计算第一次撞墙的时间，对剩余时间取模 $2\times(R-L)$ 来跳过完整的周期，再计算最后剩下的那个不完整周期内的移动，就可以算出小球的最终位置。

计算一个小球的最终位置是 $O(1)$ 的，整个算法的时间复杂度瓶颈在于排序。

时间复杂度 $O(n\log(n)+m\log(m))$。

T6

30%

修改次数最少可以转化成不修改的元素最多。如果不修改 $A_i$ 和 $A_j$ 也能让 $[L,R]$ 成为连续区间，其中 $L\leq i<j\leq R$，那么 $A_j-A_i=j-i$，移项可得 $A_j-j=A_i-i$。所以没有被修改的元素，都满足 $A_i-i$ 的值相同这一条件。

定义 $B_i=A_i-i$，定义 $g(L,R)$ 为 $\{B_L,B_{L+1},\dots,B_R\}$ 中出现最多的数字的出现次数。

因为可能出现 $A_i<i$ 的情况，所以 $B_i$ 有可能是负数，为了便于统计每种数字的出现次数，对 $B$ 数组进行处理：先求出 $B$ 数组中元素的最小值 $minB=\min \{B_i\}$，令 $B_i=B_i-minB$。处理过后的 $B_i\geq 0$，下文中的 $B_i$ 也都是做过同样处理的，不再赘述。

对于每个询问，统计 $\{B_{L_i},B_{L_i+1},\dots,B_{R_i}\}$ 中每个数字的出现次数，维护出现次数的最大值 $g(L_i,R_i)$，则答案为 $f(L_i,R_i)=R_i-L_i+1-g(L_i,R_i)$。

时间复杂度 $O(nm)$。

40%

对于测试点#4，因为 $|A_i-i|\leq 500$，所以 $B_i$ 的取值范围为 $0\sim 1000$。

记 $B_i$ 最大值为 $V=\max\{B_i\}$。

预处理 $S[x][i]$ 数组表示 $\{B_1,B_2,\dots,B_i\}$ 中数字 $x$ 出现了多少次。

对于每个询问，在 $0\sim V$ 中枚举 $x$，用差分的技巧可得 $\{B_{L_i},B_{L_i+1},\dots,B_{R_i}\}$ 中数字 $x$ 共出现了 $S[x][R_i]-S[x][L_i-1]$ 次，这样我们就可以维护出 $g(L_i,R_i)$ 并计算答案。

时间复杂度 $O((n+m)V)$。

结合第一部分可以拿到 $40\%$ 的分数。

100%

答案 $f(L_i,R_i)=R_i-L_i+1-g(L_i,R_i)$，因此我们只研究如何计算 $g(L_i,R_i)$，也就是 $\{B_{L_i},B_{L_i+1},\dots,B_{R_i}\}$ 的众数的出现次数。

区间众数问题有多种解法，这里仅介绍一种对数组进行分块的做法。

将 $B$ 按下标分块，块长度取 $\sqrt{n}$，那么块的数量为 $\lceil \frac{n}{\sqrt{n}} \rceil \approx \sqrt{n}$。

预处理 $h[i][j]$ 表示第 $i\sim j$ 块的众数的出现次数。处理方法为对于每个 $i$，将第 $i$ 块的第一个元素的下标作为左端点，让右端点逐渐向右移动，移动的同时维护每个数字的出现次数及当前众数的出现次数，当右端点为第 $j$ 块的最后一个元素的下标时记录 $h[i][j]$ 为当前众数的出现次数。

预处理 $s[x][i]$ 表示前 $i$ 块中数字 $x$ 出现了多少次。

将区间 $[L_i,R_i]$ 分成三个部分，如下图：

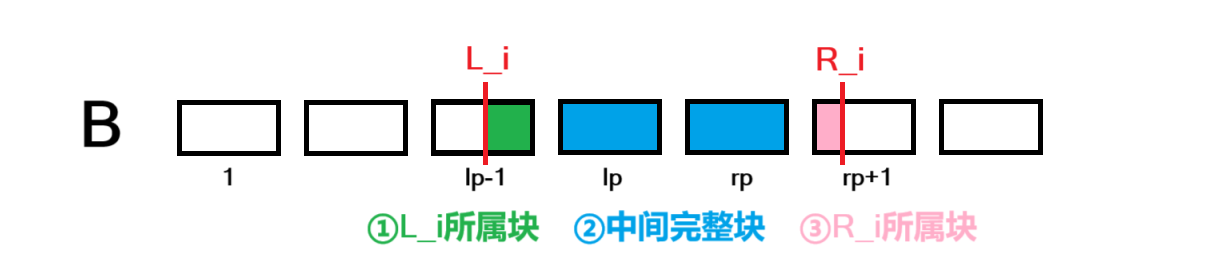
那么 $g(L_i,R_i)$ 只有两种情况：

• 如果 $\{B_{L_i},B_{L_i+1},\dots,B_{R_i}\}$ 的众数只出现在图中②部分，那么这种情况下 $g(L_i,R_i)=h[lp][rp]$；
• 否则，众数一定在①或③部分出现过，枚举在①或③部分出现过的数字 $B_j$，计算 $B_j$ 在 $\{B_{L_i},B_{L_i+1},\dots,B_{R_i}\}$ 中的出现次数。其中 $B_j$ 在①或③部分出现的次数可以直接统计，在②部分的出现次数为 $s[B_j][rp]-s[B_j][lp-1]$。

对这两种情况分别计算一个最大出现次数，两者中更大的即为 $g(L_i,R_i)$。

空间复杂度 $O(n\sqrt{n})$。

时间复杂度 $O((n+m)\sqrt{n})$。