T1

100%

不断将 $x \bmod 6$ 的余数保存起来，然后将 $x$ 除以 $6$，直到 $x$ 变为 $0$。

这样求出的是 $x$ 在六进制下从低位到高位的每一位数字，但输出的时候要从高位开始输出，所以将保存下来的余数从后往前输出。

时间复杂度 $O(\log(x))$。

T2

100%

答案分为以下两种情况：

• $x>y$，此时 $|x-y|=x-y$，当 $x$ 取最大奇数，$y$ 取最小偶数时，$|x-y|$ 最大；
• $x<y$，此时 $|x-y|=y-x$，当 $x$ 取最小奇数，$y$ 取最大偶数时，$|x-y|$ 最大；

分别求出数组 $A$ 中最大奇数 $Max_1$、最大偶数 $Max_2$、最小奇数 $Min_1$、最小偶数 $Min_2$。如果 $A$ 中同时存在奇数和偶数，答案即为 $\max(Max_1-Min_2,Max_2-Min_1)$。

注意判断 $A$ 中只有奇数或者偶数的情况。

时间复杂度 $O(n)$。

T3

50%

两重循环枚举区间左端点 $L$ 和区间右端点 $R$，如果子区间 $[L,R]$ 的区间和是 $k$ 的倍数，答案加一。

维护 $A$ 的前缀和 $s[i]=\sum_{j=1}^i A_j$，将区间和转化为两个前缀和的差分，所以只需判断 $(s[R]-s[L-1])\bmod k$ 是否等于 $0$。

时间复杂度 $O(n^2)$。

100%

$(s[R]-s[L-1])\bmod k=0$ 等价于 $(s[R] \bmod k)=(s[L-1] \bmod k)$。

因此我们只需要枚举右端点 $R$，维护 $cnt[x]$ 表示对于 $0\leq i\leq R-1$ 有多少个 $i$ 满足 $s[i] \bmod k=x$，答案增加 $cnt[s[R]\%k]$。

初始只有 $cnt[0]=1$。当右端点从 $R-1$ 变为 $R$ 时，$cnt[s[R-1]\%k]$ 需要增加一。

时间复杂度 $O(n)$。

T4

40%

记 $V=\max\{a,b,c,n,m\}$，用杨辉三角法预处理所有 $0\leq i\leq V$ 且 $0\leq j\leq i$ 的组合数 $\text{C}_i^j$。

用四重循环枚举某一类选人方案：

• 第一重循环在 $0\sim n$ 中枚举 $i_a$，表示小N老师从 $a$ 名语文好的同学中选了 $i_a$ 名；
• 第二重循环在 $0\sim n$ 中枚举 $i_b$，表示小N老师从 $b$ 名数学好的同学中选了 $i_b$ 名；
• 第三重循环在 $0\sim m$ 中枚举 $j_b$，表示小M老师从剩下 $b-i_b$ 名数学好的同学中选了 $j_b$ 名；
• 第四重循环在 $0\sim m$ 中枚举 $j_c$，表示小M老师从 $a$ 名语文好的同学中选了 $j_c$ 名；
• 如果 $i_a+i_b=n$、$j_b+j_c=m$ 且 $i_a\leq a$、$i_b+j_b\leq b$、$j_c\leq c$，说明这是一类可行的选人方案，答案增加这类方案的数量 $\text{C}_{a}^{i_a}\times\text{C}_{b}^{i_b}\times\text{C}_{b-i_b}^{j_b}\times\text{C}_{c}^{j_c}$。

时间复杂度 $O(V^2+n^2m^2)$。

60%

对于测试点#5~6，因为 $b=0$，所以小N老师只能从 $a$ 名语文好的同学中选人，小M老师只能从 $c$ 名英语好的同学中选人，答案为 $\text{C}_{a}^{n}\times \text{C}_{c}^{m}$。

时间复杂度 $O(V^2)$。

结合第一部分可以拿到 $60\%$ 的分数。

100%

观察第一部分计算一类选人方案的数量的式子，发现一类选人方案如果可行需要同时满足 $i_a=n-i_b$ 和 $j_c=m-j_b$。

因此只需要用两重循环枚举某一类选人方案：

• 第一重循环在 $0\sim n$ 中枚举 $i$，表示小N老师从 $b$ 名数学好的同学中选了 $i$ 名；
• 第二重循环在 $0\sim m$ 中枚举 $j$，表示小M老师从剩下 $b-i$ 名数学好的同学中选了 $j$ 名；
• 如果 $n-i\leq a$、$i+j\leq b$、$m-j\leq c$，说明这是一类可行的选人方案，答案增加这类方案的数量 $\text{C}_{a}^{n-i}\times\text{C}_{b}^{i}\times\text{C}_{b-i}^{j}\times\text{C}_{c}^{m-j}$。

时间复杂度 $O(V^2)$。

T5

30%

对于每个询问，两重循环枚举每一个可能被当前炸弹炸到的格子 $(px,py)$：

• 在 $\max(1,x_i-w_i)\sim \min(n,x_i+w_i)$ 范围枚举 $px$；
• 在 $\max(1,y_i-w_i)\sim \min(m,y_i+w_i)$ 范围枚举 $py$；
• 如果 $|px-x_i|+|py-y_i|\leq w_i$，说明 $(px,py)$ 会被当前炸弹炸到，答案增加 $C_{px,py}$。

时间复杂度 $O(nm+qw^2)$。

60%

当前炸弹能炸到第 $a$ 行的哪些格子。

对于 $x_i-w_i\leq a\leq x_i+w_i$，只要满足 $y_i-(w_i-|x_i-a|)\leq b\leq y_i+(w_i-|x_i-a|)$，当前炸弹就能炸到 $(a,b)$。

所以答案等于 $\sum_{px=\max(1,x_i-w_i)}^{\min(n,x_i+w_i)}\sum_{py=L(px)}^{R(px)}C_{px,py}$，其中的 $L(px)=\max(1,y_i-(w_i-|x_i-px|))$，$R(px)=\min(m,y_i+(w_i-|x_i-px|))$。

对每一行预处理格子分数的前缀和 $f[i][j]=\sum_{k=1}^j C_{i,k}$。

答案即为 $\sum_{px=\max(1,x_i-w_i)}^{\min(n,x_i+w_i)}f[px][R(px)]-f[px][L(px)-1]$。

时间复杂度 $O(nm+qw)$。

100%

炸弹能炸到的格子形成了一个近似菱形的图案。以位于 $(3，4)$ 爆炸范围为 $4$ 的炸弹为例，能炸到的格子为下图中黄色的部分（包括超出矩阵边界的）：

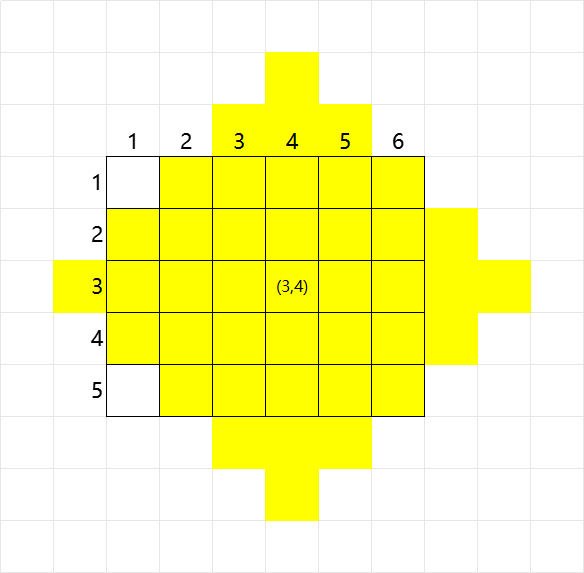
这个菱形旋转 $45$ 度后就是矩形，旋转后的坐标可以映射到“斜坐标系”上。

定义斜坐标系：格子 $(i,j)$ 位于第 $i+j$ “斜行”，第 $i-j$ “斜列”，记作 $<i+j,i-j>$。比如格子 $(3,4)$ 位于第 $7$ 斜行，第 $-1$ 斜列，记作 $<7,-1>$。

斜坐标系下格子 $<a,b>$ 的分数记作 $D[a][b]$。遍历矩阵 $C$，$D[i+j][i-j]=C[i][j]$，其余格子的分数都为 $0$。

观察可得黄色部分涉及第 $3\sim11$ 斜行的 $-5\sim 3$ 斜列。

总结出规律：对于位于 $(x，y)$ 爆炸范围为 $w$ 的炸弹，计算 $xl=(x-w)+y$、$xr=(x+w)+y$、$yl=(x-w)-y$、$yr=x-(y-w)$，炸到的格子为 $xl\sim xr$ 斜行的 $yl\sim yr$ 斜列。

定义 $g[i][j]$ 表示所有满足 $a\leq i$ 且 $b\leq j$ 的格子 $<a,b>$ 的分数之和，用二维前缀和的技巧预处理 $g[i][j]=D[i][j]+g[i-1][j]+g[i][j-1]-g[i-1][j-1]$。

对于每个询问，计算 $xl=(x_i-w_i)+y_i$、$xr=(x_i+w_i)+y_i$、$yl=(x_i-w_i)-y_i$、$yr=x_i-(y_i-w_i)$，当前询问的答案可以用二维前缀和的方法表示为 $g[xr][yr]-g[xr][yl-1]-g[xl-1][yr]+g[xl-1][yl-1]$。

其中 $xl$ 的最小值为 $(\min\{x_i\}-\max\{w_i\})+\min\{y_i\}\geq -1000$，$yl$ 的最小值为 $(\min\{x_i\}-\max\{w_i\})-\max\{y_i\}\geq -2000$，可以给坐标中的斜行加上 $1005$，斜列加上 $2005$，来让坐标都大于 $0$，相当于平移。处理 $D$ 数组和计算 $g$ 数组时，下标也做同样的平移处理。

平移后 $xr$ 的最大值为 $1005+(\max\{x_i\}+\max\{w_i\})+\max\{y_i\}\leq 4005$，$yr$ 的最大值为 $2005+\max\{x_i\}-(\min\{y_i\}-\max\{w_i\}))\leq 4005$，所以 $D$ 数组和 $g$ 数组的规模建议开到 $4010\times 4010$。

时间复杂度 $O((n+m+w)^2+q)$。

T6

20%

$dp[i][j]$ 表示从前 $i$ 种硬币中选出的总价值为 $j$ 的不同方案的数量。

用01背包的方法来转移：在 $0\sim i$ 中枚举 $k$ 表示选了 $k$ 个第 $i$ 种硬币，如果 $i\times k\leq j$ 那么 $dp[i][j]+=dp[i-1][j-i\times k]$。

注意过程中的取模和爆 $\text{int}$ 问题。

时间复杂度 $O(n^3)$。

60%

对于第 $i$ 种硬币，如果 $i\times i>n$，那么就不需要考虑这种硬币的数量限制了。

把硬币分为两类：前 $\sqrt{n}$ 种硬币称为小硬币，剩下的称为大硬币。其中大硬币是不需要考虑数量限制的。

对于小硬币，一共只有 $\sqrt{n}$ 种，$k$ 的枚举范围也不超过 $\sqrt{n}$，所以这部分的总时间复杂度为 $O(n^2)$。

对于大硬币，不需要考虑数量的限制可以视为数量无限，因此这部分可以用完全背包的方法来转移：$dp[i][j]=dp[i-1][j]+dp[i][j-i]$。这部分的总时间复杂度也为 $O(n^2)$。

时间复杂度 $O(n^2)$。

100%

先考虑小硬币：

• $f[i][j]$ 表示从前 $i$ 种硬币中选出的总价值为 $j$ 的不同方案的数量；
• $f[i][j]=f[i-1][j]+f[i-1][j-i]+\dots+f[i-1][j-i\times i]$，注意到其中第二维的下标是一个等差数列 $\{j,j-i,\dots,j-i\times i\}$；
• 对于 $i$，维护 $s[j]=f[i-1][j]+f[i-1][j-i]+\dots+f[i-1][j\mod i]$，有 $s[j]=f[i-1][j]+s[j-i]$；
• 如果 $(i+1)\times i> j$，也就是说总价值为 $j$ 时不可能用到超过 $i$ 个第 $i$ 种硬币，那么 $f[i][j]=s[j]$；
• 否则 $f[i][j]=s[j]-s[j-(i+1)\times i]$。

小硬币一共只有 $\sqrt{n}$ 种，所以这部分的总时间复杂度为 $O(n\sqrt{n})$。空间复杂度可以用滚动数组的技巧降低到 $O(n)$。

然后考虑大硬币：

• $g[i][j]$ 表示选中恰好 $i$ 个大硬币且总价值为 $j$ 的不同方案的数量；
• 如果选中了至少一个价值最低的大硬币，也就是第 $\sqrt{n}+1$ 种硬币，那么剩下 $i-1$ 个大硬币的总价值为 $j-(\sqrt{n}+1)$；
• 否则，选中的每个硬币价值都大于 $\sqrt{n}+1$，那么方案数等于每个硬币价值都减一的方案数，也就是 $i$ 个大硬币且总价值为 $j-i$；
• 因此 $g[i][j]=g[i-1][j-(\sqrt{n}+1)]+g[i][j-i]$；
• 答案增加 $g[i][j]\times f[\sqrt{n}][n-j]$，对应大硬币总价值为 $j$，小硬币总价值为 $n-j$ 的方案。

单个大硬币价值至少为 $\sqrt{n}+1$，因此选中的数量 $i$ 不可能超过 $\frac{n}{\sqrt{n}+1}\leq \sqrt{n}$，所以这部分的总时间复杂度也为 $O(n\sqrt{n})$。空间复杂度可以用滚动数组的技巧降低到 $O(n)$。

时间复杂度 $O(n\sqrt{n})$。