T1

100%

用循环模拟 $t$ 分钟的时间变化，维护当前时间 $x$ 点 $y$ 分：

• 先是分钟 $y=y+1$；
• 如果当前分钟 $y=60$，说明到了下一个小时，那么小时 $x=x+1$，分钟 $y=0$；
• 如果当前小时 $x=24$，说明到了下一天，那么小时 $x=0$。

循环 $t$ 次后的时间 $x$ 点 $y$ 分即为答案。

时间复杂度 $O(t)$。

T2

100%

两重循环枚举点 $i$ 和点 $j$，维护距离点 $i$ 最近的点的编号 $ans[i]$，距离点 $i$ 最近的点有多个时 $ans[i]$ 选其中编号最小的。

在判断距离关系时，可以直接比较距离的平方，不需要开根号。

时间复杂度 $O(n^2)$。

T3

100%

将每个订单的编号 $no$、提交时刻 $a$ 和花费时间 $t$ 三个属性放在结构体 $p$ 里，把 $p$ 按 $a$ 从小到大的顺序排序。

用循环模拟订单提交和处理的过程，维护之前提交的订单中最后一个订单完成的时刻 $now$，初始 $now=0$，对于第 $i$ 个提交的订单 $p[i]$：

• 如果 $now\leq p[i].a$，说明当前订单提交时没有正在处理的订单，那么从 $a$ 时刻开始处理当前订单，将会在 $p[i].a+p[i].t$ 时刻完成，更新最后一个订单完成的时刻 $now=p[i].a+p[i].t$；
• 如果 $now>p[i].a$，说明当前订单提交时还有其他订单正在处理，那么当前订单会取消，将当前订单的编号 $p[i].no$ 添加到数组 $ans$ 中。

循环结束后，如果数组 $ans$ 的长度为 $0$，说明没有取消的订单，输出 Perfect；否则将 $ans$ 中的元素从小到大排序后输出。

时间复杂度 $O(n\log(n))$。

T4

20%

对于求区间 $[L,R]$ 的二维异或和的询问，用两重循环分别枚举 $i$ 和 $j$ 满足 $L\leq i,j\leq R$，计算 $\sum_{i=L}^R\sum_{j=L}^R A_i\oplus A_j$。

时间复杂度 $O(qn^2)$。

60%

注意到计算两个数的异或结果 $x\oplus y$ 时，二进制下的每一位是独立的。

这意味着如果只看二进制下第 $k$ 位，$A_i$ 和 $A_j$ 不一样，那么 $A_i\oplus A_j$ 在二进制下第 $k$ 位为 $1$。如果区间 $(L,R)$ 中有 $x$ 项在这一位为 $1$，那么剩下 $(R-L+1)-x$ 项在这一位为 $0$，因此对于 $L\leq i,j\leq R$，$A_i\oplus A_j$ 在二进制下第 $k$ 位为 $1$ 的有 $x\times ((R-L+1)-x)$ 项。

定义函数 $num(L,R,i)$ 表示区间 $[L,R]$ 中有多少项在二进制下第 $i$ 位为 $1$。

对于每个询问，分别计算二进制下每一位的答案，再加起来。对于二进制下第 $i$ 位，$O(n)$ 计算 $num(L,R,i)$，答案增加 $2 \times num(L,R,i)\times ((R-L+1)-num(L,R,i))\times 2^i$。

记 $A_i$ 的最大值为 $V=\max\{A_i\}$。

时间复杂度 $O(qn\log(V))$。

100%

维护 $cnt[i][j]$ 表示区间 $[1,i]$ 中有多少项在二进制下第 $j$ 位为 $1$。

那么可以用差分的技巧 $O(1)$ 计算 $num(L,R,i)=cnt[R][i]-cnt[L-1][i]$。

时间复杂度 $O((n+q)\log(V))$。

T5

20%

时间越长每个机器人的移动范围越大，能清理的垃圾也越多，所以可以二分答案。

定义函数 $check(x)$ 来判断 $x$ 和答案的关系：

• 如果花费 $x$ 的时间无法清理所有垃圾，说明答案大于 $x$，这种情况函数返回 $0$；
• 如果花费 $x$ 的时间可以清理所有垃圾，说明答案小于等于 $x$，这种情况函数返回 $1$。

$check(x)$ 时，$1$ 类机器人和 $2$ 类机器人的移动范围是固定的，对于第 $i$ 个机器人：

• 如果是 $1$ 类机器人那么移动范围是 $a_i-x$ 到 $a_i$；
• 如果是 $2$ 类机器人那么移动范围是 $a_i$ 到 $a_i+x$。

对于测试点#1~2，只有第 $1$ 个机器人是 $3$ 类机器人，其余机器人都是 $1$ 类机器人或 $2$ 类机器人，且 $n\leq 1000$，$m\leq 2000$。因此在 $check(x)$ 时：

• 先用两重循环分别枚举第 $i$ 个垃圾和第 $j$ 个机器人：
  • 如果第 $j$ 个机器人是 $1$ 类机器人那么移动范围是 $a_j-x$ 到 $a_j$，所以如果 $a_j-x\leq b_i\leq a_j$ 说明第 $i$ 个垃圾能被第 $j$ 个机器人清理，否则说明第 $i$ 个垃圾不能被第 $j$ 个机器人清理；
  • 如果第 $j$ 个机器人是 $2$ 类机器人那么移动范围是 $a_j$ 到 $a_j+x$，所以如果 $a_j\leq b_i\leq a_j+x$ 说明第 $i$ 个垃圾能被第 $j$ 个机器人清理，否则说明第 $i$ 个垃圾不能被第 $j$ 个机器人清理；
• 如果第 $2\sim n$ 个机器人清理了所有垃圾， 说明花费 $x$ 的时间足够清理所有垃圾，$check$ 函数返回 $1$；
• 否则用第 $1$ 个机器人来清理这些没有被第 $2\sim n$ 个机器人清理的垃圾，维护这些垃圾的坐标最小值 $PL$ 和坐标最大值 $PR$，第 $1$ 个机器人的方案有两种：
  • 先清理坐标为 $PL$ 的垃圾，花费时间为 $|a_1-PL|$，再清理坐标为 $PR$ 的垃圾，花费时间为 $PR-PL$，过程中会将坐标为 $PL\sim PR$ 的垃圾一并清理掉，这个方案的总时间为 $|a_1-PL|+PR-PL$；
  • 先清理坐标为 $PR$ 的垃圾，花费时间为 $|a_1-PR|$，再清理坐标为 $PL$ 的垃圾，花费时间为 $PR-PL$，过程中会将坐标为 $PL\sim PR$ 的垃圾一并清理掉，这个方案的总时间为 $|a_1-PR|+PR-PL$；
  • 因此用第 $1$ 个机器人清理这些垃圾所需的最少时间为 $\min(|a_1-PL|,|a_1-PR|)+PR-PL$；
  • 如果 $\min(|a_1-PL|,|a_1-PR|)+PR-PL\leq x$，说明花费 $x$ 的时间足够清理所有垃圾，$check$ 函数返回 $1$；
  • 否则说明花费 $x$ 的时间不能够清理所有垃圾，$check$ 函数返回 $0$。

记坐标的最大值为 $V=\max\{a_i,b_i\}$。

时间复杂度 $O(\log(V)nm)$。

40%

对于测试点#1~4，只有第 $1$ 个机器人是 $3$ 类机器人，其余机器人都是 $1$ 类机器人或 $2$ 类机器人，因此思路还是二分答案，在 $check(x)$ 时先考虑用第 $2\sim n$ 个机器人尽可能清理垃圾，对于没有被第 $2\sim n$ 个机器人清理的垃圾，维护这些垃圾的坐标最小值 $PL$ 和坐标最大值 $PR$，用第 $1$ 个机器人在清理。

测试点#3~4的数据范围变为 $n\leq 10^5$，$m\leq 2\times 10^5$，因此我们将 $1$ 类机器人的坐标保存在数组 $Pa1$ 中，将 $2$ 类机器人的坐标保存在数组 $Pa2$ 中，并将 $Pa1,Pa2,b$ 这三个数组都从小到大排序，然后二分答案，在 $check(x)$ 时使用双指针的技巧去处理 $1$ 类机器人和 $2$ 类机器人能够清理的垃圾：

• 对于坐标第 $i$ 小的垃圾，分别找到最小的 $j_1$ 满足 $b_i\leq Pa1[j_1]$，和最小的 $j_2$ 满足 $b_i\leq Pa2[j_2]+x$：
  • 如果 $Pa1[j_1]-x\leq b_i\leq Pa1[j_1]$ 说明第 $i$ 个垃圾能被 $1$ 类机器人清理，否则说明坐标第 $i$ 小的垃圾不能被 $1$ 类机器人清理；
  • 如果 $Pa2[j_2]\leq b_i\leq Pa2[j_2]+x$ 说明第 $i$ 个垃圾能被 $2$ 类机器人清理，否则说明坐标第 $i$ 小的垃圾不能被 $2$ 类机器人清理；
• 如果 $1$ 类机器人和 $2$ 类机器人清理了所有垃圾， 说明花费 $x$ 的时间足够清理所有垃圾，$check$ 函数返回 $1$；
• 否则尝试用唯一的 $3$ 类机器人来清理这些没有被 $1$ 类机器人和 $2$ 类机器人清理的垃圾，参考第一部分。

时间复杂度 $O((n+m)\log(V))$。

60%

对于测试点#5~6，所有机器人都是 $3$ 类机器人，因此先将 $a$ 数组和 $b$ 数组都从小到大排序后，再二分答案，在 $check(x)$ 时使用双指针的技巧，尝试用剩余机器人中坐标最小的去清理剩余垃圾中坐标最小的：

• 如果坐标第 $1\sim i-1$ 小的垃圾已经用坐标第 $1\sim j-1$ 小的机器人清理了，那么考虑坐标第 $i$ 小的垃圾用坐标第 $j$ 小的机器人来清理；

• 如果 $|b_i-a_j|>x$，说明坐标第 $i$ 小的垃圾无法用坐标第 $j$ 小的机器人清理，继续尝试用坐标第 $j+1$ 小的机器人来清理这个垃圾；

• 否则坐标第 $i$ 小的垃圾可以用坐标第 $j$ 小的机器人清理，考虑让这个机器人在清理这个垃圾的同时，尽可能清理更多垃圾，也就是求出这个机器人在需要移动到 $b_j$ 的前提下，能移动到的最大坐标 $FR$，并用这个机器人将坐标为 $a_j\sim FR$ 的垃圾一并清理掉；

• 如果 $a_j\leq x$，那么这个机器人会一直向右移动，$FR=a_j+x$；

• 否则这个机器人的方案有两种：

  • 先向左移动到 $b_i$ 再向右移动，$FR=\max(a_j,b_i+(x-(a_j-b_i)))$；
  • 先向右移动再向左移动到 $b_i$，$FR=a_j+\frac{x-(a_j-b_i)}{2}$；

• 如果坐标第 $1\sim m$ 小的垃圾可以用坐标第 $1\sim n$ 小的机器人清理，$check$ 函数返回 $1$；否则 $check$ 函数返回 $0$。

时间复杂度 $O((n+m)\log(V))$。

结合第二部分可以拿到 $60\%$ 的分数。

100%

将第二部分与第三部分相结合：

• 将 $1$ 类机器人的坐标保存在数组 $Pa1$ 中，将 $2$ 类机器人的坐标保存在数组 $Pa2$ 中，将 $3$ 类机器人的坐标保存在数组 $Pa3$ 中，并将 $Pa1,Pa2,Pa3,b$ 这四个数组都从小到大排序，然后二分答案；
• 在 $check(x)$ 时：
  • 先处理 $1$ 类机器人和 $2$ 类机器人能够清理的垃圾，参考第二部分；
  • 再尝试用 $3$ 类机器人来清理这些没有被 $1$ 类机器人和 $2$ 类机器人清理的垃圾，参考第三部分。

时间复杂度 $O((n+m)\log(V))$。

T6

40%

对于第 $i$ 个炸弹，从节点 $p_i$ 出发进行 $\text{DFS}$ 将所有满足 $dis(p_i,j)\leq w_i$ 的节点 $j$ 的答案 $ans[j]$ 都增加 $1$。

时间复杂度 $O(nm)$。

100%

将节点 $1$ 定义为树的根，把树转化为有根树。

定义函数 $fa(x,i)$ 表示从节点 $x$ 向根节点方向移动 $i$ 次后到达的节点。如果节点 $x$ 到根节点的距离 $dis(x,1)<i$，定义 $fa(x,i)=0$。

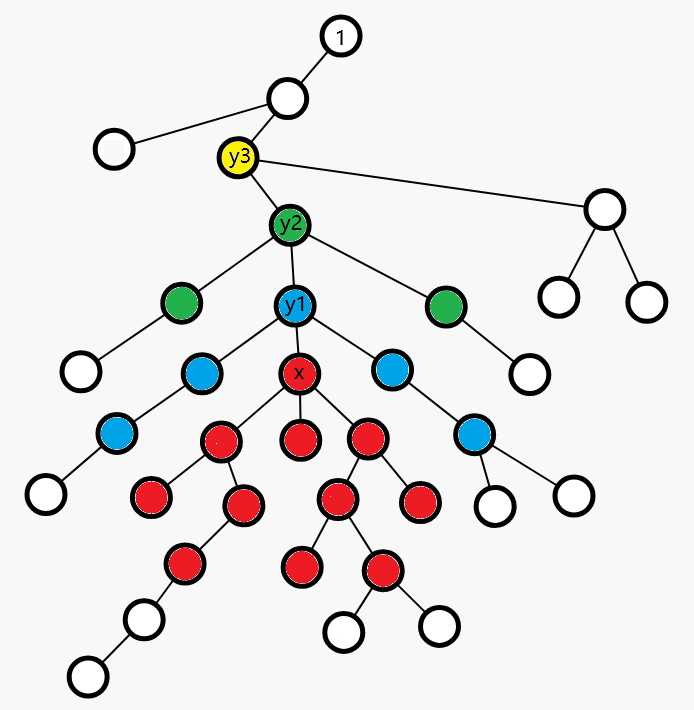
对于上图，$fa(x,0)=x$，$fa(x,1)=y_1$，$fa(x,2)=y_2$，$fa(x,3)=y_3$。

考虑在节点 $x$ 放置一个爆炸范围 $w=3$ 的炸弹，分析这个炸弹所造成的影响：

• 首先以节点 $x$ 为根的子树中，与节点 $x$ 距离不超过 $3$ 的节点都会被炸一次，如上图中红色部分；
• 以节点 $y_1$ 为根的子树中，与节点 $y_1$ 距离不超过 $2$ 的且不在以节点 $x$ 为根的子树中的节点都会被炸一次，如上图中蓝色部分；
• 以节点 $y_2$ 为根的子树中，与节点 $y_2$ 距离不超过 $1$ 的且不在以节点 $y_1$ 为根的子树中的节点都会被炸一次，如上图中绿色部分；
• 节点 $y_3$ 会被炸一次，如上图中黄色部分；

定义 $f[x][i]$ 表示以节点 $x$ 为根的子树中，与节点 $x$ 距离不超过 $i$ 的节点都会被炸一次。

先处理炸弹，对于炸弹 $i$：

• 以节点 $p_i$ 为根的子树中，与节点 $p_i$ 距离不超过 $w_i$ 的节点都会被炸一次，即 $dp[p_i][w_i]+=1$；
• 枚举 $0< j< w_i$，如果 $fa(p_i,j)\neq 0$，那么以节点 $fa(p_i,j)$ 为根的子树中，与节点 $fa(p_i,j)$ 距离不超过 $w_i-j$ 的且不在以节点 $fa(p_i,j-1)$ 为根的子树中的节点都会被炸一次：
  • 先让以节点 $fa(p_i,j)$ 为根的子树中，与节点 $fa(p_i,j)$ 距离不超过 $w_i−j$ 的节点都被炸一次，即 $dp[fa(p_i,j)][w_i-j]+=1$；
  • 对于涉及到的以节点 $fa(p_i,j-1)$ 为根的子树中的节点，用树上差分的技巧进行抵消：令以节点 $fa(p_i,j-1)$ 为根的子树中，与节点 $fa(p_i,j-1)$ 距离不超过 $w_i-(j+1)$ 的节点都少被炸一次，即 $dp[fa(p_i,j-1)][w_i-(j+1)]-=1$；
• 如果 $fa(p_i,w_i)\neq 0$，那么节点 $fa(p_i,w_i)$ 会被炸一次，即 $dp[fa(p_i,w_i)][0]+=1$。

处理完所有炸弹后，从节点 $1$ 出发进行 $\text{DFS}$，遍历一次整棵树。遍历的过程中维护 $f[x][i]+=f[fa(x,1)][i+1]$。

完成遍历后，节点 $i$ 的答案 $ans[i]=\sum f[i][j]$。

时间复杂度 $O(50(m+n))$。